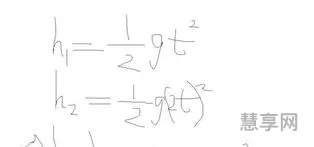样本方差公式(样本方差要除以n—1)
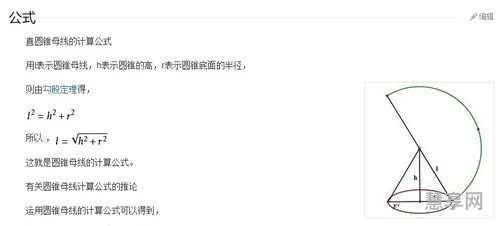
样本方差公式
即偏离平方的均值,记为E(X):直接计算公式分离散型和连续型。推导另一种计算公式得到:“方差等于各个数据与其算术平均数的离差平方和的平均数”。其中,分别为离散型和连续型计算公式
例如两人的5次测验成绩如下:X:50,100,100,60,50,平均值E(X)=72;Y:73,70,75,72,70平均值E(Y)=72。平均成绩相同,但X不稳定,对

方差的计算公式提供了一种测度数据偏离程度的方法,可以帮助我们评估数据的变化范围。在实际应用中,方差经常被用于建模、预测以及其他数据分析方面。学会使用方差的计算公式D(x)可以使我们在实际应用中更加健全地使用数据分析。
假设我们有一个包含n个数据点的数据集{X1,X2,X3,,Xn},那么该数据集的平均值可表示为mean:
综上所述,方差计算公式需要根据具体的情况来进行选择。对于总体方差,分母使用n;对于样本方差,分母使用n-1。这也是为什么在统计分析中常常有这样的说法,“样本均值的自由度为n-1”。
样本方差要除以n—1
根据传统的定义,样本方差使用n-1作为分母来计算,而总体方差使用n作为分母来计算。这是由于样本方差和总体方差的推导过程不同,而且由于使用n-1会减小方差的大小,因此样本方差比总体方差更能够反映样本内部的数据分布情况。
需要先求出这组数据的均值。均值的计算公式是所有数据的和除以数据的个数。然后,需要计算每个数据与均值的差,并将差值平方。将每个差的平方加起来,然后再除以数据的个数,即可得到方差。
方差是统计学中常用的一种测度数据偏离程度的方法,在数据分析中有着广泛的应用。方差的计算公式通常表示为D(x),表示数据集中所有数据与平均值的平均偏差的平方。下面我们具体介绍一下该公式的具体计算方法。
例如,有一组数据:6,8,7,5,9。它们的均值是7。求每个数据与均值的差,可以得到-1,1,0,-2,2。然后将差的平方分别计算出来,即1,1,0,4,4。将它们加起来得到10,再除以数据的个数5,最终得到方差为2。
需要注意的是,方差的计算公式中有一个平方运算,这意味着方差的单位与原始数据单位的平方相同。因此,在使用方差进行比较时,需要注意数据的单位是否相同。
D(X)与E(X)公式
然后我们需要计算(X1-mean),(X2-mean),(X3-mean),,(Xn-mean)的平方和,并将其除以n即可得到方差。
方差广泛应用于各种领域,如经济、***、生物、社会科学等。通过计算方差,我们可以分析数据的集中程度和分散程度,从而更好地理解数据。
方差是用来衡量数据分散程度的一种统计量。在对数据的分散程度进行度量时,常用的方法是计算样本方差和总体方差。在计算方差时,需要注意的一个关键性问题就是方差计算公式是否使用n还是n-1。
需要注意的是,分母是n-1而不是n。这是因为我们在用样本来估计总体方差时,会有一定的误差。如果分母是n,则估计结果会偏小,因此使用n-1来纠正这种偏差。