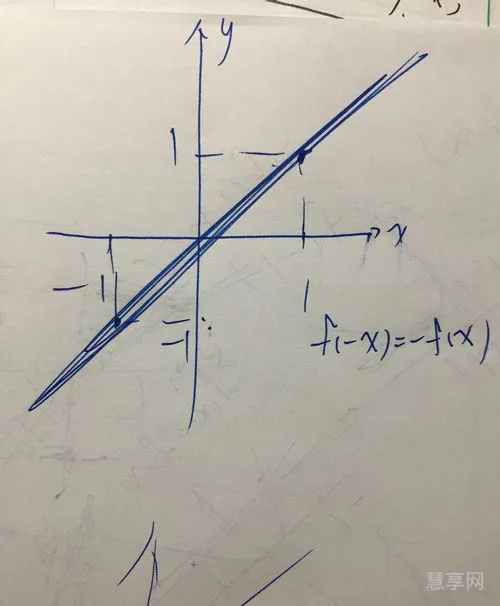怎么判断奇函数(怎么一眼看出函数的奇偶性)

怎么判断奇函数

一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=-f(x),那么函数f(x)就叫奇函数。

根据分解的函数之间的运算法则判断,一般只有三种种f(x)g(x)、f(x)+g(x),f(g(x))(除法或减法可以变成相应的乘法和加法);

定义法:对于f(x)定义域A内的任意一个x,如果都有f(——x)=——f(x),那么f(x)为奇函数;如果都有f(——x)=f(x),那么f(x)为偶函数。

偶函数:假如一个函数g(x)的定义域关于原点对称,并且对于定义域中的任意x都有g(-x)=g(x),则称函数g(x)为偶函数。

怎么一眼看出函数的奇偶性

注意:定义域关于原点对称是函数具有奇偶性的前提。如果一个函数的定义域不关于原点对称,则这个函数一定不具有奇偶性。

奇偶性的判断方法共有五种,分别为定义法、求和(差)法、求商法、图像观察法以及函数运算法则来判断。下面我们就来看一看,判断函数奇偶性的一般步骤是什么?

若f(x)、g(x)其中一个为奇函数,另一个为偶函数,则f(x)g(x)奇、f(x)+g(x)非奇非偶函数,f(g(x))奇;

一般地,如果对于函数f(x)的定义域内任意一个x,都有f(-x)=f(x),那么函数f(x)就叫偶函数。

函数的奇偶性口诀

奇函数:假如一个函数f(x)的定义域关于原点对称,并且对于定义域中的任意x都有f(-x)=-f(x),则称函数f(x)为奇函数。

所以它如果在0处有定义,函数值一定为0,也就是函数过原点。但不定积分的结果是一系列函数,并不是每一个都过原点,因此偶函数的不定积分不一定为奇,仅过原点的为奇。

奇函数是指定义域关于原点对称的函数f(x)的定义域中的任意X都有f(-x)=-f(x),所以函数f(x)称为奇函数。

1727年,年轻的瑞士数学家欧拉为了解决“反弹问题”,在提交给圣彼得堡科学院的论文(拉丁文)中首次提出了奇偶函数的概念。