奇函数的定义(奇函数的性质有哪些)

奇函数的定义

1727年,年轻的瑞士数学家欧拉为了解决“反弹问题”,在提交给圣彼得堡科学院的论文(拉丁文)中首次提出了奇偶函数的概念。

奇函数是指定义域关于原点对称的函数f(x)的定义域中的任意X都有f(-x)=-f(x),所以函数f(x)称为奇函数。

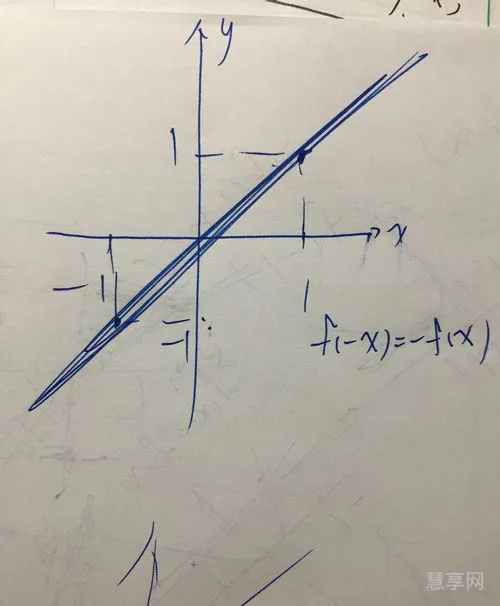
如果仔细研究近几年的高考数学试卷,不难发现函数奇偶性这一题每年都会考,题型多样,侧重点不同。函数是高中数学的重要内容之一,而奇偶性实际上是一个图像关于原点或者Y轴的对称性,所以在图形别明显,在函数的学习中起着非常重要的作用。

常用待定系数法:F(x)f(-x)=0用来生成关于字母的恒等式,从系数的等价性可以知道字母的值。

奇函数的性质有哪些

根据奇函数像关于原点的对称性,奇函数在原点两侧对称区间内具有相同的单调性;根据偶函数关于Y轴的像的对称性,在原点两侧对称区间内,偶函数的单调性是相反的。

如果函数f(x)的定义域中任意x有f(-x)=-f(x),则函数f(x)是奇函数。该图像的特点是关于原点对称。

如果函数的定义域关于原点对称,则可以进一步判断F(-x)=-f(x)或F(-x)=f(x)对于定义域中的每一个x是否为常数(常数待定,或给出反例)。

如果函数满足f(x+t)=f(x),从函数周期性的定义可以知道,t是函数的一个周期;需要注意的是,nT(n∈Z,n≠0)也是函数的周期。

什么叫做奇函数

【注意】判断分段函数的奇偶性,要分段证明f(-x)与f(x)之间的关系,只有每段上的x满足相同的关系,才能判断其奇偶性。

在奇偶性和单调性的综合中,要注意奇函数在关于原点对称的区间内具有相同的单调性,而偶函数在关于原点对称的区间内具有相反的单调性。

对于函数y=f(x),如果有一个非零常数t,使得当x在定义域取任意值时,有f(x+t)=f(x),则函数y=f(x)称为周期函数,t称为这个函数的周期。

函数奇偶性是NMET数学考试的常见考点。这类题的考点主要考察奇函数和偶函数的定义及其等价形式,以及函数奇偶性和函数其他性质的综合应用。因此,我们必须掌握奇函数和偶函数的定义及其等价形式,以及函数的其他性质。