利用三角形全等测距离(hl证明三角形全等怎么得到的)
利用三角形全等测距离
三组对应边分别相等的两个三角形全等(简称sss或“边边边”),这一条也说明了三角形具有稳定*的原因。

s.a.(angle-side-angle)(角、边、角):各三角形的其中两个角都对应地相等,且两个角夹着的边都对应地相等的话,该两个三角形就是全等。
直角三角形全等条件有:斜边及一直角边对应相等的两个直角三角形全等(hl或“斜边,直角边”)所以,sss,sas,asa,aas,hl均为判定三角形全等的定理。
a.a.(angle-angle-angle)(角、角、角):各三角形的任何三个角都对应地相等,但这并不能判定全等三角形,但则可判定相似三角形。
3)遇到角平分线在三种添辅助线的方法,(1)可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的*质定理或逆定理.(2)可以在角平分线上的一点作该角平分线的垂线与角的两边相交,形成一对全等三角形。(3)可以在该角的两边上,距离角的顶点相等长度的位置上截取二点,然后从这两点再向角平分线上的某点作边线,构造一对全等三角形。
hl证明三角形全等怎么得到的
a.s.(angle-angle-side)(角、角、边):各三角形的其中两个角都对应地相等,且没有被两个角夹着的边都对应地相等的话,该两个三角形就是全等。
角度数为30、60度的作垂线法:遇到三角形中的一个角为30度或60度,可以从角一边上一点向角的另一边作垂线,目的是构成30-60-90的特殊直角三角形,然后计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角。从而为*全等三角形创造边、角之间的相等条件。
5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关*质加以说明.这种作法,适合于*线段的和、差、倍、分等类的题目。
全等三角形:三角形是特殊的多边形,因此,全等三角形的对应边、对应角分别相等。同样,如果两个三角形的边、角分别对应相等,那么这两个三角形全等。
2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”法构造全等三角形。
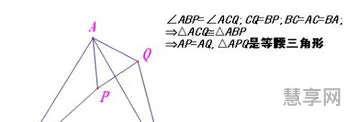
三角形内PA十PB十PC的最小值
计算数值法:遇到等腰直角三角形,正方形时,或30-60-90的特殊直角三角形,或40-60-80的特殊直角三角形,常计算边的长度与角的度数,这样可以得到在数值上相等的二条边或二个角,从而为*全等三角形创造边、角之间的相等条件。
s.s.(side-side-side)(边、边、边):各三角形的三条边的长度都对应地相等的话,该两个三角形就是全等。
确定已知条件(包括隐含条件,如公共边、公共角、对顶角、角平分线、中线、高、等腰三角形、等所隐含的边角关系);