等边三角形的判定(怎么证明是等边三角形)
等边三角形的判定
首先,我们知道等边三角形的特征是三条边长度相等,因此我们可以通过已知的BC长度推出AB的长度为8。然后,根据等边三角形的性质,可以得出角AOB为120度,进而通过三角函数的关系式计算出角AOC、BOE等角度,最终得出DE/BE=√3/2,进而可以求出BE的长度为6/√3。最终,可以得出AB的长度为8+12=20。
由此可见,等边三角形的应用非常广泛,是中小学数学教学中的重要内容。只要熟练掌握其特征和性质,并善于应用,就能在解决各种数学问题时得心应手。
等边三角形可以用来衡量三角形中各个参数的值,如以等边三角形为基准,计算其他三角形的周长、面积、角度等参数。
在$△ABC$中,∵$∠A=∠B=∠C$,∴$△ABC$为等边三角形B.在$△ABC$中,∵$AB=AC$,且$∠B=∠C$,∴$△ABC$为等边三角形C.在$△ABC$中,∵$∠A=60°$,$∠B=60°$,∴$△ABC$为等边三角形D.在$△ABC$中,$∵AB=AC$,$∠B=60°$,∴$△ABC$为等边三角形
怎么证明是等边三角形
解析:$∠A=∠B=∠C$,所以$△ABC$为等边三角形,故A选项正确;$AB=AC$且$∠B=∠C$,$△ABC$不一定是等边三角形,故B选项错误;$∠A=60°$,$∠B=60°$,三个内角都是60°,所以$△ABC$为等边三角形,故C选项正确;$AB=AC$,$∠B=60°$,三个内角都是60°,所以$△ABC$为等边三角形,故D选项正确。故选B。
等边三角形的性质和定义,一、等边三角形的性质和定义1、等边三角形三条边都相等的三角形叫等边三角形。其三个内角相等,均为60°,它是锐角三角形的一种。等边三角形是特殊的等腰三角形,它拥有等腰三角形的一切性质。2、等边三角形的性
金字塔:在建筑领域,等边三角形被广泛用于设计金字塔和其他类型的建筑物,这种形状的稳定性使其成为建造高大建筑物的理想选择。
等边三角形的内角都相等,且均为60°。等边三角形三边相等,三个角也相等。每个三角形内角和都为180度,所以等边三角形每个角都是60度,它是锐角三角形的一种。等边三角形也是最稳定的结构。等边三角形是特殊的等腰三角形,所以等边三角形拥有等腰三角形的一切性质。
等边三角形有几种证法
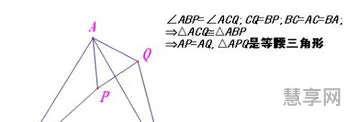
为了证明这一点,我们可以使用几何证明的方法。首先,在等边三角形ABC中,我们可以假设AB=BC=CA,并且∠A=∠B=∠C。因为AB=BC,所以∠A=∠B。因为BC=CA,所以∠B=∠C。因此,我们可以得出∠A=∠B=∠C。而根据三角形内角和定理,三个内角的和为180度。所以每个内角的度数是180度除以3,即60度。综上所述,等边三角形的内角度数为60度。
钟表:大多数钟表的面设计为圆形,这是因为圆是最简单的闭合曲线,可以方便地划分出相等的时间间隔。然而,为了方便阅读,钟表的小时和分钟刻度通常以等边三角形的形式呈现。
量角器:等边三角形的每个内角都是60度,因此可以用来测量角度。量角器是一种用来测量角度的工具,其基本原理就是利用等边三角形的这个性质。
等边三角形的内角度数都是60度。在等边三角形中,三条边的长度相等,三个内角的度数也相等。根据三角形内角和定理,一个三角形的三个内角之和为180度。