倾斜角与斜率(斜率和倾斜角对应表)
倾斜角与斜率
内,当直线l与x轴相交时,我们取x轴作为基准,x轴正向与直线l向上方向之间所成的角a叫做直线l的倾斜角(angleofinclination)
斜率,亦称“角系数”,表示一条直线相对于横轴的倾斜程度。一条直线与某平面直角坐标系横轴正半轴方向的夹角的正切值即该直线相对于该坐标系的斜率。如果直线与x轴垂直,直角的正切值无穷大,故此直线不存在斜率。当直线L的斜率存在时,对于一次函数y=kx+b(斜截式),k即该函数图像(直线)的斜率。
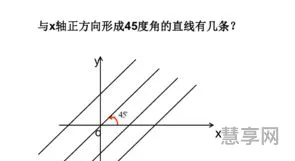
两直线的倾斜角不相等,则它们的斜率也一定不相等;两直线的倾斜角相等,则它们的斜率要么存在且相等,要么都不存在。
通过空间游戏,学习立体搭建,积木类、磁力贴类开放性玩具,也是培养“空间思维”的最佳玩具。年龄小的孩子,可以在爸爸妈妈的帮助下,学习爸爸妈妈的样子。你先搭好一个样子,让孩子依样画葫芦也搭一个。
直线对X轴的倾斜角α的正切值tgα称为该直线的“斜率”,并记作k,k=tgα。规定平行于X轴的直线的斜率为零,平行于Y轴的直线的斜率不存在。
斜率和倾斜角对应表
倾斜角是函数图像上某点的切线与x轴的夹角,每给一个点就有其对应的倾斜角,而斜率是该倾斜角的正切值,即若倾斜角表示为α,斜率为tanα
使用空间语言,掌握空间名词,空间语言是空间学习的重要基础。和孩子的日常沟通中,当空间关系被命名时,孩子学相关内容会更快。
平面直角坐标系中,直线不与x轴平行或重合时必与x轴相交。此时,以x轴为基准,x轴正向与直线向上的方向之间所成的角叫作直线的倾斜角。
它有无数条对称轴,其中一条是它本身,还有所有与它垂直的直线(有无数条)对称轴。在平面上过不重合的两点有且只有一条直线,即不重合两点确定一条直线。在球面上,过两点可以做无数条类似直线。
在最开始的时候,家长们可以在带着孩子爬楼梯的时候,教他认识上和下的概念、高和低的区别,在外出的时候,学习左和右,前和”,融入各种方位描述。平时陪孩子玩耍时,可以把在这里、在那里用具体的方位词描述出来,如,在沙发左边、在中间抽屉里。
斜率和倾斜角的关系图
曲线的变化趋势仍可以用过曲线上一点的切线的斜率即导数来描述。导数的几何意义是该函数曲线在这一点上的切线斜率。
当直线倾斜角α从90°增大到180°时,斜率k从“负无穷大”增大到0。即α∈(90°,180°)时,k∈(-∞,0)。
(4)两直线的倾斜角不相等,则它们的斜率也一定不相等;两直线的倾斜角相等,则它们的斜率要么存在且相等,要么都不存在。







