正三棱锥的性质(正三棱锥的面积公式)
正三棱锥的性质
正四面体在数学中广泛应用于对称群的研究,以及在拓扑学和代数学中的一些难题中解决关键性问题。在物理学中,正四面体可用于描述晶体结构以及杂化化合物的分子结构。此外,正四面体还可以应用于计算机图形学和计算机视觉中。
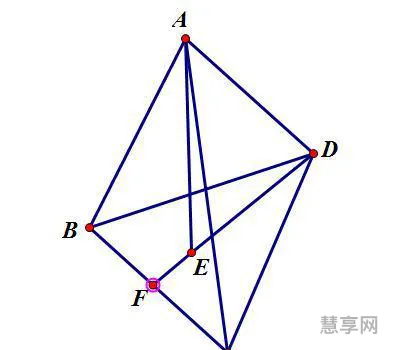
正三棱锥是一种四面体,它有一个三角形底面和三条共边而均等的三角形侧壁面,因此它也常被称为等角三棱锥。正三棱锥是拥有所有三种三角形都共存的最简单的几何体之一,具有10个对称操作。
正四面体和正三棱锥是两种具有重要特点和特性的多面体。它们在许多领域都有各自的应用和价值。了解这些形状的属性和特点,有助于我们更好地理解和利用它们,进而拓展应用领域和解决实际问题。
正三棱锥在工程学中具有广泛的应用,例如构建物体的强度良好的纤维强化材料。此外,在建筑设计和雕塑领域,正三棱锥也常被用作基本图形。
正三棱锥的面积公式
在几何学中,正四面体和正三棱锥是两种常见的几何体。它们都具有一些特殊的性质和特点,因此被广泛应用于各种领域,包括数学、物理和工程学等。
正四面体是一种多面体,它有四个等边、等角的三角形面,四个顶点围成了一个等角四面体。它的对称性非常高,具有24个对称操作。正四面体是最简单的拓扑四面体,因其形状特殊而成为重要的几何体。
正四面体:正四面体是由四个全等正三角形围成的空间封闭图形,所有棱长都相等。它有4个面,6条棱,4个顶点。正四面体是最简单的正多面体,同时也是一种特殊的正三棱锥。
正四面体所有边都等长,而正三棱锥只有三条侧棱等长、底面的三条边等长,正三棱锥的侧棱长并不一定等于地面边长。正四面体是特殊的正三棱锥。
正三棱锥对棱互相垂直
正三棱锥:正三棱锥是立体几何名词,是锥体中的一种底面是等边三角形,三个侧面是全等的等腰三角形的三棱锥。
数学中只有三棱锥和四面体,这两者本质上是没有区别的,三角锥只是一种特殊说法。三棱锥是锥体的一种,由四个三角形组成,称为四面体。底面是正三角形,顶点在底面的射影是底面三角形的中心的三棱锥,称作正三棱锥。
若O是△ABC的外心,则OA=OB=OC。由于OP⊥平面ABC(射影的定义),因此OP⊥OA、OP⊥OB、OP⊥OC。勾股定理得PA=PB=PC。又tanPAO=OP/OA,tanPBO=OP/OB,tanPCO=OP/OC,由此可知∠PAO=∠PBO=∠PCO。