自然数是指哪些数字(什么叫做自然数)

自然数是指哪些数字

自然数是数学中最基本的数字,它们是从1开始,一直到无穷大的数字。自然数可以用来表示物体的数量,也可以用来表示某件事情发生的次数。自然数也可以用来表示一个数字的位置,比如第一个,第二个,第三个等等。

自然数也可以用来表示一个数字的大小,比如1比2小,2比3小,3比4小等等。自然数也可以用来表示一个数字的增加或减少,比如1加1等于2,2减1等于1等等。

自然数可以分为奇数和偶数,奇数是从1开始,一直到无穷大的所有奇数,而偶数是从2开始,一直到无穷大的所有偶数。自然数也可以分为素数和合数,素数是只能被1和它本身整除的自然数,而合数是可以被1和它本身以外的数整除的自然数。

自然数是数学中最基本的数字,它们可以用来表示物体的数量,某件事情发生的次数,一个数字的位置,大小,增加或减少,因数,倍数等等。自然数是数学中最基本的数字,它们是从1开始,一直到无穷大的数字,是数学中最重要的数字。

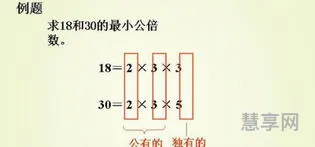
自然数也可以用来表示一个数字的因数,比如6的因数是1,2,3,6,而8的因数是1,2,4,8等等。自然数也可以用来表示一个数字的倍数,比如2的倍数是2,4,6,8,10等等。

什么叫做自然数

其次,在实际应用中也能够证明1是最小的自然数。在现代科学、工程和技术领域中,很多问题都需要使用数字来进行计算和分析。而在这些问题中,“0”通常被用作起点或基准值。,在计算机科学中,“0”通常被用作数组和列表中元素位置的起点;在物理学和工程学中,“0”通常被用作测量过程中某个物理量的基准值。因此,在这些领域中,1作为最小的自然数,也可以被证明是正确的。

需要注意的是,在这些扩展概念中,并不存在“第二个”或“第三个”元素等类似于“第二个自然数”或“第三个自然数组合”的概念。这是因为这些不再具有像自然数组合那样的有限性质。

我们可以采用反证法来证明1是最小的自然数。假设存在另外一个比1更小的正整数k,则k必须大于0且小于等于1。因为k小于等于1,则k只能取值为0或者1;而k又必须大于0,则k只能取值为1。所以,不存在比1更小的自然数,因此1是最小的自然数。

其次,最小的自然数也是一些重要规律和公式中的关键元素。,在排列组合中,当我们从n个不同元素中选取k个元素时,总共有C(n,k)种不同方案。而当k=0时,只有一种方案,即一个元素也不选;当k=n时,则只有一种方案,即选取所有元素。这些特殊情况下对应的组合数量都是由1来确定的。

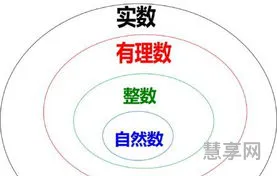
(2)实数:实数包括有理数和无理树两部分。在实际应用中,我们通常将自然数看作是实数中的一部分,而最小的自然数1也是实数中的最小正整数。

0是否属于自然数

在数学中,自然数是由0开始递增的整数序列。那么,我们如何证明1是最小的自然数呢?本文将从两个方面进行探讨。

自然数是指从1开始,依次递增的正整数,即1,2,3,4,。自然数是最基本的数字概念之一,它们在各个领域中都有着广泛的应用。

自然数是指从1开始的整数序列,其中最小的自然数就是1。虽然1看似微不足道,但它在数学中却具有重要意义。

最小自然数1是自然数中最小的一个,而负整数和实数则是自然数的扩展。在负整数和实数中,也有类似于最小自然数的概念。

自然数是我们在日常生活中经常接触到的一种数学概念,它包括了0、1、2、3等无限个正整数。然而,对于自然数的最小值,却有着一个令人困惑的问题: