最小的自然数是几(小学最小的数是0还是1)
最小的自然数是几
自然数的有序性是指,自然数可以从0开始,不重复也不遗漏地排成一个数列:0,1,2,3等,这个数列叫自然数列。一个集合的元素如果能与自然数列或者自然数列的一部分建立一一对应,我们就说这个集合是可数的,否则就说它是不可数的。自然数的无限性是指自然数集是一个无穷集合,自然数列可以无止境地写下去。
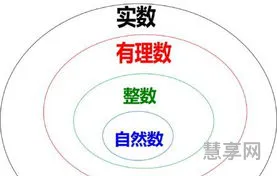
自然数由0开始,一个接一个,组成一个无穷的集体,一个物体也没有,可以用0表示,所以最小的自然数是0,没有最大的自然数,自然数的个数是无限的。自然数是指用以计量事物的件数或表示事物次序的数。即用数码0,1,2,3,4所表示的数。
在数学中,自然数是由0开始递增的整数序列。那么,我们如何证明1是最小的自然数呢?本文将从两个方面进行探讨。
我们可以采用反证法来证明1是最小的自然数。假设存在另外一个比1更小的正整数k,则k必须大于0且小于等于1。因为k小于等于1,则k只能取值为0或者1;而k又必须大于0,则k只能取值为1。所以,不存在比1更小的自然数,因此1是最小的自然数。
小学最小的数是0还是1
?这个问题看似简单,实则涉及到了自然数的定义及其性质。在本文中,我们将会简要介绍自然数的定义与性质,并探讨如何证明1是最小的自然数。同时,我们也会探讨最小自然数在数学中的重要性以及与其他概念(如负整数、实数等)之间的关系。此外,文章末尾还会提供与最小自然数相关的习题及解答。
(2)实数:实数包括有理数和无理树两部分。在实际应用中,我们通常将自然数看作是实数中的一部分,而最小的自然数1也是实数中的最小正整数。
自然数是我们在日常生活中经常接触到的一种数学概念,它包括了0、1、2、3等无限个正整数。然而,对于自然数的最小值,却有着一个令人困惑的问题:
其次,最小的自然数也是一些重要规律和公式中的关键元素。,在排列组合中,当我们从n个不同元素中选取k个元素时,总共有C(n,k)种不同方案。而当k=0时,只有一种方案,即一个元素也不选;当k=n时,则只有一种方案,即选取所有元素。这些特殊情况下对应的组合数量都是由1来确定的。
0到底算不算自然数
首先,对于负整数而言,它们是自然数的相反数。,-1是1的相反数。在负整数中,存在一个最大的元素,即最大负整数。与最小自然数类似,在证明过程中需要使用归纳法来证明这一点。可以通过定义一个新的序列来证明:-1,-2,-3,…,其中每个元素都比前一个元素小1。因此,在负整数中存在一个最大元素。
自然数是指从1开始,依次递增的正整数,即1,2,3,4,。自然数是最基本的数字概念之一,它们在各个领域中都有着广泛的应用。
最小自然数1是自然数中最小的一个,而负整数和实数则是自然数的扩展。在负整数和实数中,也有类似于最小自然数的概念。
自然数是指从1开始的整数序列,其中最小的自然数就是1。虽然1看似微不足道,但它在数学中却具有重要意义。