sin60度等于多少啊

sin60度等于多少啊

sin60度等于:√3/2。对于任意直角三角形,假设斜边为c,60°角的对边为b,则sin60°=b/c=√3/2。正弦是指在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA,即sinA=∠A的对边/斜边。

通过这种方法,我们可以很容易地求出其他角度的正弦值,只要根据三角形的定义,并利用三角函数的性质,就可以准确地得到正确的*。

在数学的初中阶段,学生通常都需要学习sin、cos、tan三个函数的定义、性质、图象等方面的内容。同时,学生也需要掌握它们的数值表达方式,最常见的方法是利用三角函数表进行查找和计算。

在数学中,三角函数是极为重要的概念之一。三角函数有很多种,其中最基础的三角函数之一就是正弦函数。而要计算正弦函数的值,就需要知道角度。角度是以360度作为一个整体的,一种度量角度大小的方法。那么,我们如何计算三角函数中的角度呢?

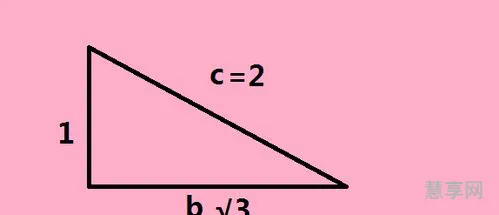
举例来说,我们要计算sin60度等于多少。我们知道,sin60度代表一个角度大小,意味着在一个角为60度的三角形中,对着60度这条边的直角边的长度与斜边长的比值。这可以用一个简单的分数来表示,即sin60度=√3/2。

30°,45°,60°角的三角函数值

这道题的计算可以用三角形来解决。以60度角为顶角,做一个边长为1的等边三角形。设其底边中点为M。由于容易从正方形中求得在每个等腰直角三角形中,斜边等于以下值之一:1、√2、2的其中之一。这个等边三角形中斜边是1,则每个等腰直角三角形中,斜边都是√3。连接点M和底边的端点,则角AMN为30度,角M为60度。于是,由三角形的正弦定义可得,sin60度=斜边/1=√3/2。

sin60度等于多少啊,是一个数学问题。在三角函数中,正弦(sin)是一个常用的三角函数,它表示一条角度为θ的直角三角形中,对边长度与斜边长度之比。在这个问题中,θ等于60度,因此我们需要计算60度角的正弦值。

sin60度等于0.866025,可以表示60度角的正弦值,也可以表示等边三角形中高与边长的比值。这个问题虽然简单,但是展示了数学中一些基础的概念和计算方法。

正弦是与一个角度的对边比上斜边得出的一个三角函数值,它是三角函数中的一员。在一个60度的直角三角形中,可以根据正弦公式计算出正弦值。角度为60度的三角形有一个相邻角度为30度,它是一个特殊的三角形,其中包含一个以1为边长的等边三角形和三个60度的相等角度。在这个三角形中,对于60度的角度,它的对边长度为1,而斜边长度为2,因此根据正弦公式sin60度=1/2√3。

三角函数是数学中非常重要的概念之一,包括正弦函数(sin)、余弦函数(cos)、正切函数(tan)等。它们在数学、物理、工程等领域的应用非常广泛。

三角函数值对照表

正弦函数在数学和物理中具有广泛的应用。例如在声学中,正弦函数可以描述声音在空气中的传播;在数学中,正弦函数是平面上的周期函数,被广泛用于解决方程和计算函数极值等问题。因此,了解和熟练掌握正弦函数的计算方法是很重要的。

使用三角函数表或计算器可以得知,sin60度的值为0.866025。换句话说,在一个角度为60度的直角三角形中,其对边长度为斜边长度的0.866025倍。

此外,sin60度还有一种特殊的含义。60度是等边三角形的内角之一,因此sin60度可以表示等边三角形的高与边长之比。等边三角形的三条边和三个角都相等,因此它的高和边长的比例也相同,都是根号三的二分之一。因此,sin60度等于根号三的二分之一,也就是0.866025。

三角函数表中列出了一些常见的角度值(例如0°、30°、45°、60°、90°等),以及这些角度对应的sin、cos、tan的具体数值。和其他数学表格一样,正确使用三角函数表需要先确定所需要的输入(例如角度值),再在表格中进行查找,***得到相应的输出(例如sin值)。

Sin60度等于0.8660。这个角度的意义是,等边三角形的内角***的一个。这个角度在圆形领域中表现的非常明显,因为它是以60度为间隔的,也就是说,圆形中有6个等分的角度,每个角度大小为60度。