长方体和正方体的表面积(正方体长方体全部公式)

长方体和正方体的表面积

正方体是特殊的长方体,它虽然也有长宽高,但它们之间是相等的,所以,在正方体里,叫做棱长。长方体由于长宽高并不等,所以会造成三种不同的面,而正方体则只有一种相同面。

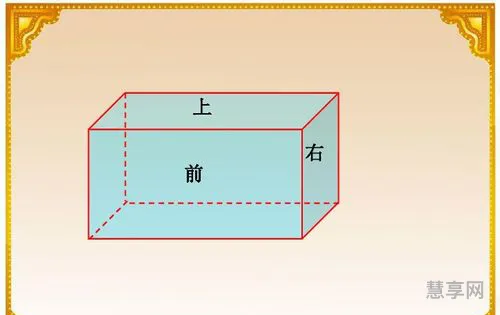
长方体或正方体的各个表面的面积相加之和叫做表面积。它们的公式如下:长方体表面积=(长x宽+长x高+宽x高)x2,正方体表面积=棱长x棱长x6。

设长方体的长、宽、高分别为A、B、C,则它的表面积为S=(abbcca)2,也等于2abBCCA和2(abBCCA);公式:长方体表面积=长宽2宽高2长高2,或长方体表面积=(长宽高长高)2。

长方体是一种常见的几何体,其表面积是指长方体外侧所有面积的总和。在日常生活和工作中,人们常常需要计算长方体表面积,例如在建筑设计、包装设计、物流运输等方面,都需要对长方体表面积进行计算。本文将从多个角度分析长方体表面积的意义、计算方法、应用场景和优化方法。

正方体长方体全部公式

长方体表面积是指长方体外侧所有面积的总和,其中包括6个面,分别为长方形的两个底面、四个侧面。长方体表面积是长方体的重要参数之一,它可以反映出长方体的大小、形状和表面特征,是对长方体进行计算和分析的基础。

长方体表面积的计算方法比较简单,可以通过公式进行计算。假设长方体的长、宽、高分别为a、b、c,则长方体表面积S的计算公式为:

包装设计:在包装设计中,包装箱的表面积是一个重要参数,需要根据产品的尺寸和数量计算出来,以便确定包装箱的大小和材料用量。

改变长、宽、高的比例:通过改变长、宽、高的比例,可以找到一种最优的比例,使得长方体表面积最小,从而达到优化的目的。

关于长方体和正方体的手抄报

其中,2ab、2bc、2ac分别代表长方体的两个底面和四个侧面的面积。需要注意的是,在计算长方体表面积时,要先确定长、宽、高的大小关系,以免计算错误。

增加高,减少长或宽:同样,在保持长方体体积不变的情况下,增加高,减少长或宽,也可以有效减少表面积。

长方体表面积的优化方法主要是通过改变长、宽、高的比例来减少表面积。一般来说,长方体的表面积越小,所需的材料和成本就越少。下面是几种常见的优化方法: