扇形面积怎么求(求扇形面积的3个公式)

扇形面积怎么求

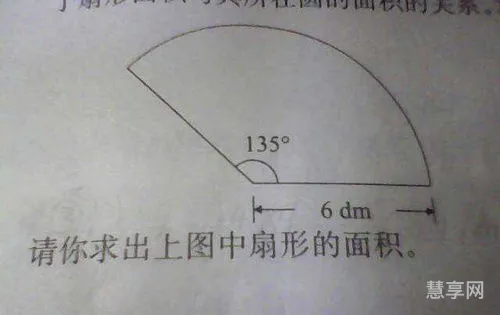
扇形是一个图形,由一个半径为r的圆中,沿着圆心角θ上的弧线所夹的区域组成。这个图形可以用扇形面积计算公式来计算它的面积。扇形面积公式是:

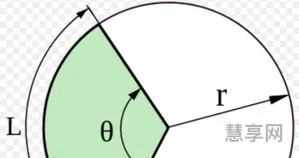
在天文学中,扇形面积公式可以被用来计算星系,星团和行星的质量。对于测量天空上的角度以及距离一些天体的距离也是很有帮助的。

在工程中,扇形面积公式被用于计算锅炉和压力容器的大小,以及测量风扇机组的能力和热损失。它还用于计算气旋和流体力学中的辐散物质体。

扇形是常见的一个图形,它的面积可以通过扇形面积计算公式来计算。使用扇形面积公式时,需要知道扇形的半径和圆心角度数,并将这些值代入公式中计算。这个公式在许多领域中都得到了广泛应用。

在日常生活中,扇形面积的计算可以被用来计算图形的面积,例如风扇的叶片和轮胎的橡胶磨损程度。它也是几何学和物理学中许多问题的基础。

求扇形面积的3个公式

使用扇形面积计算公式首先要找出扇形的半径和圆心角度数。其次,将这些值代入公式中计算出扇形的面积。在计算时要注意度数要转换成弧度。弧度是一个角度的度数除以180度乘以π。

其中r是圆的半径,θ是圆心角的度数。扇形面积计算公式的推导可以通过将扇形分成三个部分来完成:圆心角所对应的扇形面积、与圆心角相邻的三角形、和与扇形相邻的小三角形。这三个部分的面积加起来就是扇形的面积。

除法的性质:在除法里,被除数和除数同时扩大(或缩小)相同的倍数,商不变.0除以任何不是0的数都得0.

圆柱的表面积:圆柱的表面积等于底面的周长乘高再加上两头的圆的面积.公式:S=ch+2s=ch+2πr2

12.分数大小的比较:同分母的分数相比较,分子大的大,分子小的小.异分母的分数相比较,先通分然后再比较;若分子相同,分母大的反而小.

扇形面积πrl

11.分数的加减法则:同分母的分数相加减,只把分子相加减,分母不变.异分母的分数相加减,先通分,然后再加减.

等式:等号左边的数值与等号右边的数值相等的式子叫做等式.等式的基本性质:等式两边同时乘以(或除以)一个相同的数,等式仍然成立.

乘法分配律:两个数的和同一个数相乘,可以把两个加数分别同这个数相乘,再把两个积相加,结果不变.如:(2+4)×5=2×5+4×5.

分数的加、减法则:同分母的分数相加减,只把分子相加减,分母不变.异分母的分数相加减,先通分,然后再加减.

例3:两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。如右图那样重合.求重合部分(阴影部分)的面积。