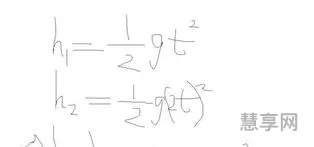三角形的面积公式是什么(三角形计算公式大全)

三角形的面积公式是什么

勾股定理(毕达哥拉斯定理)内容为:在任何一个直角三角形中,两条直角边的长平方之和一定等于斜边长的平方。

三角形的面积计算公式为:三角形底乘以高除以2。可知:底×高=2面积;底=三角形面积×2÷高;高=三角形面积×2÷底。(面积=底×高÷2。其中,a是三角形的底,h是底所对应的高)。

计算三角形面积公式是:三角形面积=1/2X底X高,或者说,三角形面积=(底X高)÷2。S=a(底)Xb(高)÷2,其中,a是三角形的底,h是底所对应的高。三角形面积是指一个三角形通过测量和计算而得的平面面积。

公式一是面积=底x高/2,这个公式主要应用于知道三角形的底和高的情况,只要将底和高相乘再除以2就可以求出面积。

三角形面积最常用的面积公式:S=(底x高)÷2=(1/2)x底x高。这里的“底”可以为三角形三条边中的任意一条边,而高则是顶点到底边的距离。

三角形计算公式大全

三角形面积公式:S=(底x高)÷2=(1/2)x底x高。【注】(1)三角形ABC的任何一条边都可以作底;(2)顶点到“底”的距离称为三角形的“高”。

三角形的面积计算公式为:三角形底乘以高除以2。已知三角形底为a,高为h,则S=ah/2。已知三角形两边为a,b,且两边夹角为C,则三角形面积为两边之积乘以夹角的正弦值,即S=(absinC)/2。

三角形面积公式有三种,分别是通过底边和高的关系计算、通过三边长度计算(海伦公式)、通过正弦关系可以计算三角形的面积。

三角形的面积计算公式是:面积=底边×高÷2。确定三角形的底边和高。底边是三角形的任意一条边,高是从底边到与底边垂直的顶点的线段。测量底边的长度。使用尺子或测量,将底边的长度测量出来。

S△=1/2*a*h,a——底边长,h——高;S△=1/2*a*b*sinC,a、b——三角形两条边长,C——两边的夹角;S△=√[p(p-a)(p-b)(p-c)],a、b、c——三角形三条边长,p=(a+b+c)/2。

三角形面积公式sin cos

三角形面积公式:面积=底×高÷2,S=ah/2(其中,a是三角形的底,h是底所对应的高)注释:三边均可为底,应理解为:三边与之对应的高的积的一半是三角形的面积。

三角形的面积公式:三角形的面积可以通过多种方法计算,其中最常用的是以下公式:三角形面积=0.5*底边长度*高,其中底边长度为三角形底边的长度,高为从底边到对边的垂直距离。

三角形的面积公式:S=ah/2(其中S表示三角形的面积,a表示三角形的一边,h表示a边上的高);S=absinC/2(其中S表示三角形的面积,a,b分别表示三角形的两边,C表示a,b两边的夹角)。

三角形的面积计算公式为S=ah/2,(a为底、h为高)。假设一个三角形的底为6米,高为4米,那么他的面积S=(4×6)/2=12米。

三角形面积计算公式如下:海伦公式:√p×(p-a)×(p-b)×(p-c):海伦公式是三角形面积计算中比较高级的方法之一,适用于已知三角形三边长度的情况。