圆周率是什么(3,1415926535.....全部)
圆周率是什么
小于4。接着,他对内接正六边形和外接正六边形的边数分别加倍,将它们分别变成内接正12边形和外接正12边形,再借助勾股定理改进圆周率的下界和上界。他逐步对内接正多边形和外接正多边形的边数加倍,直到内接正96边形和外接正96边形为止。最后,他求出圆周率的下界和上界分别为223/71和22/7,并取它们的平均值3.141851为圆周率的近似值。阿基米德用到了
宗教巨著《百道梵书》(SatapathaBrahmana)显示了圆周率等于分数339/108,约等于3.139。
和圆周率有关。例如,金字塔的周长和高度之比等于圆周率的两倍,正好等于圆的周长和半径之比。公元前800至600年成文的
一块古巴比伦石匾(约产于公元前1900年至公元前1600年)清楚地记载了圆周率=25/8=3.125。
埃及人似乎在更早的时候就知道圆周率了。英国作家JohnTaylor(1781—1864)在其名著《金字塔》(《TheGreatPyramid:Whywasitbuilt,andwhobuiltit?》)中指出,造于公元前2500年左右的
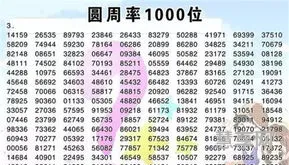
3,1415926535.....全部
文物,莱因德数学纸草书(RhindMathematicalPapyrus)也表明圆周率等于分数16/9的平方,约等于3.1605。
由此得到圆周率的上下界。他取半径为1尺,由圆内接正6边形面积开始,逐步算得正96边形和正192边形面积为
在西欧,文艺复兴后,才有人在圆周率π值上做出达到和超过祖冲之的工作。第一个得到祖冲之密率355/113的是德国人V.奥托(1573)。法国F.韦达用古典方法计算到正3×217边形求π值到10位数字(1579)。荷兰L.范.科伦在1596年求到小数点后20位,才超过卡西。
H.朗伯在1767年证明圆周率π是无理数,即不能表示成有理分数,因而不会是有限小数或循环小数。F.von林德曼在1882年证明π是超越数,即不是任何一元有理系数多项式的根。从而解决了古代三大几何难题之一──化圆为方不可能用尺规作图作出。
电子计算机发明以后,π值的计算得到飞速的发展。在1949年计算到2037位,1959年计算到16167位,1967年计算到50万位,1974年计算到100万位,1981年计算到200万位,1983年计算到223(800多万)位。
圆周率200位背诵口诀
欧拉在1748年出版的《无穷小分析引论》中提出三角函数是对应的函数线与圆半径的比。他同时引入角的弧度制,即取圆半径作为单位,圆心角用其所对的弧长表示。这时平角所对的半圆周长是π。从此以后圆周率π就作为相当于180°的角度值。
计算π值到100位小数(1706)。W.香克斯在1873年利用梅钦公式计算π值到707位小数,以后长期保持这个记录。但在1946年D.F.弗格森发现香克斯的第528位错了。他后来和美国J.W.小雷恩在1948年联合发表808位准确的π值。
记忆圆周率对于锻炼大脑的作用很像体育锻炼对于身体各部分机能的*和健康的作用。如同疲劳的体力劳动不能代替体育锻炼一样,工作中不断处理“伤脑筋”的事并不能代替对于大脑的锻炼。
要记忆上百位、上千位的无理数,完全靠机械记忆是不容易的,在记忆过程中,自觉不自觉地要用一些记忆数字的方法,而且很可能找到一些自己独创的方法。







