绝对值的定义(绝对值的方程式的解法)

绝对值的定义

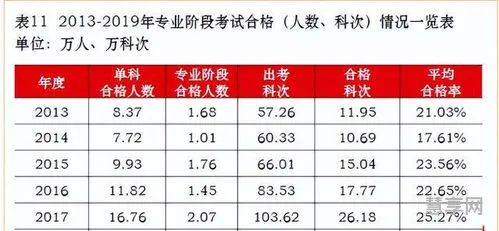
绝对值(absolutevalue)是指一个数在数轴上所对应点到原点的距离,用“||”来表示。|b-a|或|a-b|表示数轴上表示a的点和表示b的点的距离。在数学中,绝对值或模数|x|为非负值,而不考虑其符号,即|x|=x表示正x,|x|=-x表示负x(在这种情况下-x为正),|0|=0。例如,3的绝对值为3,-3的绝对值也为3。数字的绝对值可以被认为是与零的距离。

绝对值是有理数这一章的重要概念,它的应用非常多。学生掌握了绝对值的概念之后,要求学生能够求出一个数的绝对值。今后,学生还会学习求一个式子的绝对值和求无理数的绝对值。

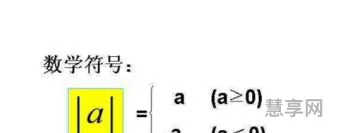
绝对值是指一个数在数轴上所对应点到原点的距离,用"||"来表示。|b-a|或la-bl表示数轴上表示a的点和表示b的点的距离。在数学中,绝对值或模数|x|的非负值,而不考虑其符号,即x|=x表示正x,Ix|=-x表示负x(在这种情况下-x为正),10|=0。例如,3的绝对值为3,-3的绝对值也为3。数字的绝对值可以被认为是与零的距离。

在数学中,绝对值或模数|x|的非负值,而不考虑其符号,即|x|=x表示正x,|x|=-x表示负x(在这种情况下-x为正),|0|=0。例如,3的绝对值为3,-3的绝对值也为3。数字的绝对值可以被认为是与零的距离。

绝对值的方程式的解法

利用几何知识求解,绝对值指的是在数轴上,点到原点的距离。我们可以拓展一下,x-3的绝对值表示的是x与3之间的距离;那么x+6的绝对值表示的是x与-6之间的距离,这样问题就转化成了,在数轴上有一点(表示的数为x)到3与-6的距离之和为9,确定这点x的取值范围。

例如,给学生的命题是|-3|的绝对值是多少?对于实数学生会很容易得出*,在答对之后,教师就可以把3换成字母a,让学生解答|-a|的绝对值是多少?在是数字的时候,*会非常的清晰,而换成字母的时候,之前有数字命题的过渡,能够让学生解题起来更有思路。

例如:两个学生从校门口出发分别往东走了40米,另一名学生往西走了50米,问题是,他们谁离学校的距离更远?如果在数轴上看的话,学校是原点,向东走就是正数方向,向西走是负数方向,用有理数表示就是一个是+40,另一个是-50,按照正负数考虑,肯定是40要大于-50,但是,如果按照距离来测量,是没有正数与负数之分的,这里的正确*就要运用到绝对值的相关概念,是向西走了50米的同学离学校远。

例指出下列问题中哪些是变量,它们之间的关系用什么方式表达:1火车的速度是每小时60千米,在t小时内行过的路程是s千米;2用表格给出的某水库的存水量与水深;3等腰三角形的顶角与一个底角;4由某一天气温变化的曲线所揭示的气温和时刻.

绝对值的化简方法口诀

数轴是最原始的将“数”和“形”结合在一起的数学知识,在此问题中学生不仅能用代数知识和几何图形知识解决这个问题,还对绝对值又有了进一步的理解,更重要的是学生有了初步“代数”与“几何”结合思想的认识。

(1)数形结合。中学教学的基本知识可分为三类:一是数形结合的知识,主要表现为解析几何;二是纯粹的形知识;三是纯粹数知识。数形结合作为一种数学思想方法,主要包括“以数辅形”和“以形助数”。其主要应用表现为:或应用数字的精确性,阐述形的某些属性,数为手段,形为目的;或是借助生动的形阐述数之间的关系,形为手段,数为目的。

小结:在实际生活中,有时存在这样的情况,无需考虑数的正负性质,比如:在计算小狗所跑的路程中,与小狗跑的方向无关,这时所走的路程只需用正数,这样就必须引进一个新的概念?———绝对值。

代数解法:根据题中给出的已知条件,可以求出经过A(-4,-1)和B1(2,-5)的一次函数解析式,再求出一次函数解析式与y轴的交点坐标,这个坐标即为所求的P点坐标,点P为(0,-■)。