空间几何体的直观图(立体图形的直观图)

空间几何体的直观图

长度减半,平行于x轴和z轴的线段长度不变)来掌握. (2)按照斜二测画法得到的平面图形的直观图,其面积与原图;【变式训练】;解析:根据题

面垂直,又底面也是长方形,符合长方体的定义,正确.故选D.;【题后反思】;【变式训练】; 解析:对于A,正四棱柱必须满足底面是正方形的直棱柱,

第六章;课标要求;名称;名称;[注意]常见的几种四棱柱的结构特征及其之间的关系;名称;名称;2.直观图;;【名师点睛】;考点一空间几何体的结构特征;3棱台的上、下底面可以不相似,但侧棱长一定相等.; 图6-1-1

S圆台=π(r'2+r2+r'l+rl)(r',r分别为上、下底面半径,l为母线长).;2圆柱、圆锥、圆台的体积

(1)圆锥、圆柱的侧面展开图分别为扇形和矩形,圆锥、圆柱的底面周长分别为扇形的弧长、矩形的一边长,据此建立圆锥、圆柱基本量的联系解决问题.

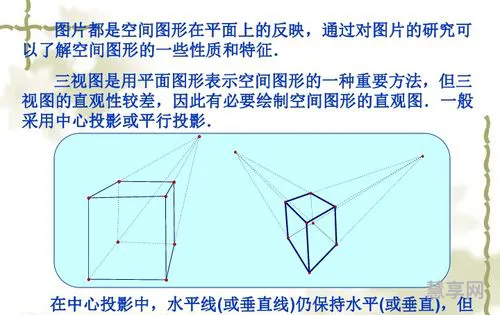
立体图形的直观图

该课程不在平台退款保障范围内,不支持退款。如需退款请联系机构老师,与机构自行协商沟通,达成一致后由机构主动发起退款

指数函数的概念:一般地,函数叫做指数函数(exponential),其中x是自变量,函数的定义域为R。

对于函数不同的单调递增(减)区间,千万记住,不要使用并集,指明这几个区间是该函数的单调递增(减)区间即可。

课内重视听讲,课后及时复习。新知识的接受,数学能力的培养主要在课堂上进行,所以要特点重视课内的学习效率,寻求正确的学习方法。上课时要紧跟老师的思路,积极展开思维预测下面的步骤,比较自己的解题思路与教师所讲有哪些不同。

函数及其定义域是不可分割的整体,没有定义域的函数是不存在的,因此,要正确地写出函数的解析式,必须是在求出变量间的对应法则的同时,求出函数的定义域。求函数的定义域一般有三种类型:

什么叫做直观图

设A、B是非空的数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A-B为从集合A到集合B的一个函数,记作y=f(x),xA

(3)如果y=f(u),u=g(x),那么y=f[g(x)]叫做f和g的复合函数,其中g(x)为内函数,f(u)为外函数、

(2)方程0)(xf有实根函数(yfx)的图像与x轴有交点函数(yfx)有零点。因此判断一个函数是否有零点,有几个零点,就是判断方程0)(xf是否有实数根,有几个实数根。函数零点的求法:解方程0)(xf,所得实数根就是(fx)的零点(3)变号零点与不变号零点

“包含”关系—子集注意:有两种可能(1)A是B的一部分,;(2)A与B是同一集合。反之:集合A不包含于集合B,或集合B不包含集合A,记作AB或BA