协方差的意义(协方差反映了什么)
协方差的意义
我们一直在讨论一个随机变量的情况,一个随机变量的均值,一个随机变量的方差,当涉及到两个随机变量的时候,有时候我们要判定他们两个的相关性,协方差的意义就在于此。
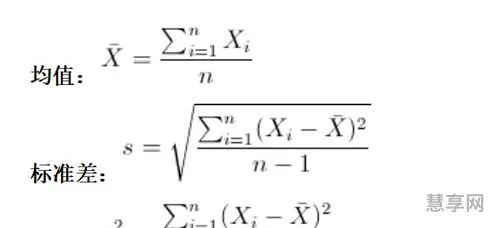
好了,最后,我觉得理解协方差矩阵的关键点在于理解多维随机变量,不同维度之间的协方差,对应起来就是协方差矩阵的元素。
方差呢就是描述样本稳定性的,比如你的成绩,一会儿全班第一,一会儿不及格,这就是方差很大。张三总是在班级前十,但也没当过第一,这方差就比较小。
学过概率统计的孩子都知道,统计里最基本的概念就是样本的均值,方差,或者再加个标准差。首先我们给你一个含有n个样本的集合,依次给出这些概念的公式描述,这些高中学过数学的孩子都应该知道吧,一带而过。
4.2不能处理非线性流形(manifold)的问题【线性流形和非线性流形,特征选择是线性降维吗】
协方差反映了什么
协方差就是衡量多维数据集中,变量之间相关性的统计量。比如说,一个人的身高与他的体重的关系,这就需要用协方差来衡量。如果两个变量之间的协方差为正值,则这两个变量之间存在正相关,若为负值,则为负相关。
马氏距离也可以定义为两个服从同一分布并且其协方差矩阵为的随机变量X和Y的差异程度或者数据点x和y之间的马氏距离。
可以看到样本基本服从f(x)=x的线性分布,A与B相对于原点的距离依旧相等,显然A更像是一个离群点。
(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的(scale-invariant),即*于测量尺度。【考虑特征之间的相关性有什么意义呢】
马氏距离(MahalanobisDistance)是一种距离的度量,可以看作是欧氏距离的一种修正,
协方差cov与相关系数
里面有求逆矩阵的过程,不满秩不行,要求数据要有原维度个特征值,如果没有可以考虑先进行PCA,这种情况下PCA不会损失信息。
数据过采样的话,需要计算距离的样本更多的是处于少数类中,又是特征选择问题,其实很容易出现特征数大于样本数的情况,此时,协方差如何计算?
先举个比较常用的例子,身高和体重,这两个变量拥有不同的单位标准,也就是有不同的scale。比如身高用毫米计算,而体重用千克计算,显然差10mm的身高与差10kg的体重是完全不同的。但在普通的欧氏距离中,这将会算作相同的差距【如果说归一化之后还会有影响吗】;
不受量纲的影响,两点之间的马氏距离与原始距离的测量单位无关;由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。马氏距离还可以排除相关性的干扰。







